Puertas lógicas
# Introducción
Al igual que con los números en base 10 o en decimal, con los números binarios se puede operar, es decir realizar operaciones con ellos como las aritméticas básicas suma, resta, multiplicación y división. De hecho el procedimiento para hacerlo es exactamente el mismo que en decimal, sólo que respetando las características de este sistema de numeración, es decir, trabajar con sólo dos cifras.
Pero no es de ese tipo de operadores de los que queremos hablar, sino de los operadores de una rama de las matemáticas llamada álgebra de Boole o booleana (en honor a su autor George Boole (opens new window)). Esta rama define las reglas de la lógica, es decir el campo de lo verdadero y lo falso.
Todos los operadores de Boole se pueden construir fácilmente en electrónica. Es a estos dispositivos a los que llamamos puertas lógicas que es donde se reunen el sistema de numeración binario con la electrónica y la informática. Asimilando los conceptos de 0 a Falso y 1 a Verdadero y aprovechando las leyes enunciadas por Boole veremos que con unos pocos operadores básicos podremos construir otros más complejos y poco a poco cualquier calculador que nos propongamos. Éste es el fundamento último de los sistemas digitales como por ejemplo los ordenadores.
# Estados lógicos
Antes de ver los operadores, vamos a describir los estados básicos de la lógica que precisamente vamos a manipular con los operadores que veremos después.
- Verdadero: Representa lo cierto o correcto, como la misma palabra indica. Será el resultado de una comparación favorable (por ejemplo
2 es menor que 3). - Falso: Representa la no certeza o lo incorrecto como también la propia palabra expresa. Será el resultado de una comparación desfavorable (por ejemplo
3 es menor que 0).
Podemos establecer una correspondencia o equivalencia entre los estados lógicos Verdadero y Falso y las cifras de un número binario o bit 1 y 0. En ambos casos tenemos dos estados mútuamente excluyentes. En electrónica estos valores 0 y 1 se manejan con tensiones eléctricas. En Arduino por ejemplo 0 equivale a 0V (o GND de Ground o Tierra en inglés) y 1 a 5V.
De hecho vamos a empezar representando la equivalencia de los estados lógicos en el terreno de la electrónica.
# Verdadero
Representará la conducción de la corriente eléctrica. Será equivalente a un contacto o interruptor cerrado. Así la tensión a la entrada se encuentra a la salida.
# Falso
Representará la no conducción de la corriente eléctrica. Será equivalente a un contacto o interruptor abierto. Así la tensión a la entrada no se traslada a la salida.
# Puertas lógicas
Vamos pues a ver ya las operaciones de las que estamos hablando que trabajarán sobre los dos estados lógicos definidos anteriormente. Como hemos comentado en la introducción, a los operadores lógicos de Boole implementados electrónicamente se les llaman Puertas Lógicas. En general definiremos una puerta mediante lo que llamaremos su tabla de verdad que representará las posibles combinaciones de las entradas con su valor a la salida.
# Negación (NOT)
Esta puerta lógica es la única de las que vamos a ver que sólo tiene una entrada y niega o invierte el valor de dicha entrada. En escritura lo representaremos con la palabra NOT ("no" en inglés).
Simbólicamente lo representaremos con el siguiente pictograma:
Electricamente es equivalente a:
Representa un interruptor que se mantiene cerrado en reposo y se abre cuando es activado. Para entender el circuito anterior como un operador NOT hay que interpretar los dos estados posibles de la entrada a, activo o inactivo (1 ó 0). Si actuamos sobre a se desplaza el interruptor y por tanto el contacto se abre. En estado inactivo sucede lo contrario. Vemos pues que de alguna forma el estado de la entrada (a) se invierte en la salida (b).
Su tabla de verdad es:
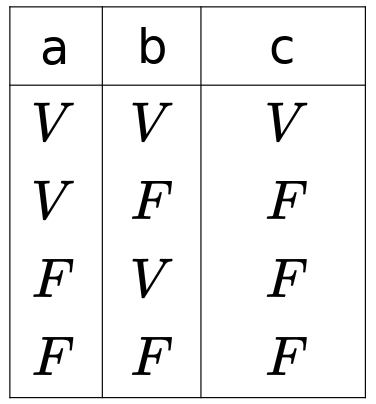
# Conjunción (AND)
Esta puerta lógica tiene dos entradas y básicamente activa la salida sólo cuando las dos entradas están activas. En escritura lo representaremos con la palabra AND ("y" en inglés).
Simbólicamente lo representaremos con el siguiente pictograma:
Eléctricamente es equivalente a:
Como vemos se corresponde con dos interruptores en serie que se cierran al ser activados. Si actuamos sobre ninguno o sólo uno de los dos interrupotores, el circuito queda abierto. Vemos pues que la salida indica si estamos activando a Y b.
Su tabla de verdad es:
# Disyunción (OR)
Esta puerta lógica tiene dos entradas y básicamente activa la salida cuando cualquiera de las dos entradas están activas. En escritura lo representaremos con la palabra OR ("o" en inglés).
Simbólicamente lo representaremos con el siguiente pictograma:
Eléctricamente es equivalente a:
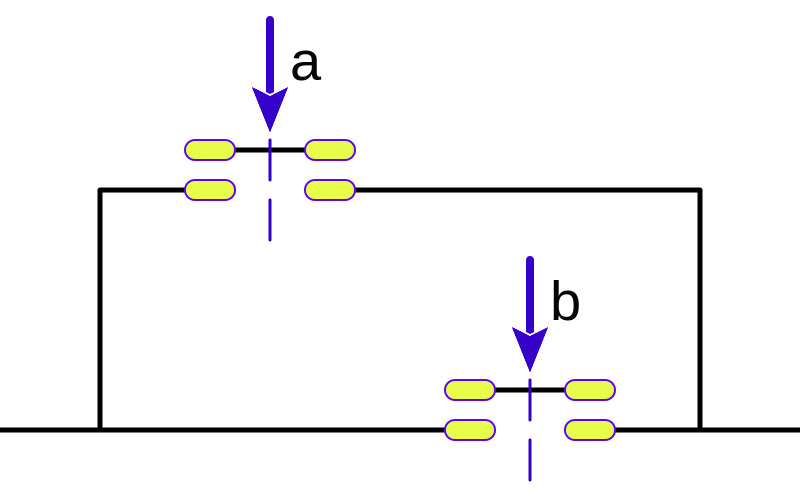
Como vemos se corresponde con dos interruptores en paralelo que se cierran al ser activados. Si actuamos sobre cualquiera de los dos interruptores, el circuito queda cerrado. Vemos pues que la salida indica si estamos activando a O b.
Su tabla de verdad es:
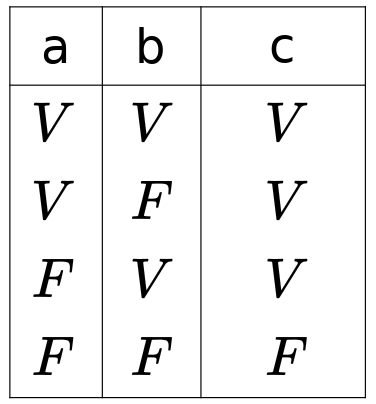
# Disyucción exclusiva (XOR)
Esta puerta lógica tiene dos entradas y básicamente activa la salida cuando las entradas tienen distinto valor entre sí. En escritura lo representaremos con la palabra XOR (contracción de "exclusive or" en inglés).
Simbólicamente lo representaremos con el siguiente pictograma:
Eléctricamente es equivalente a:
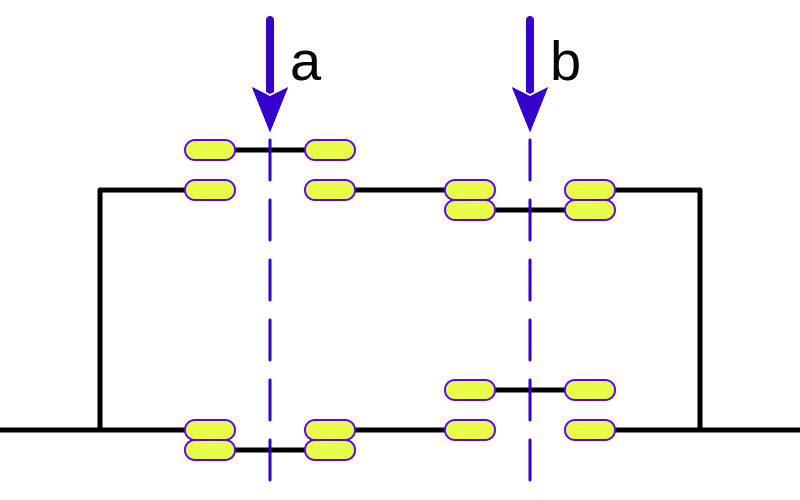
Como vemos se corresponde con dos interruptores en paralelo de doble vía en disposición opuesta de manera que si ambas señales están activadas o desactivadas el circuito siempre está abierto por alguno de los lados. Sin embargo actuando sólo en una de las entradas se alinean alguna de las dos ramas paralelas.
Su tabla de verdad es:
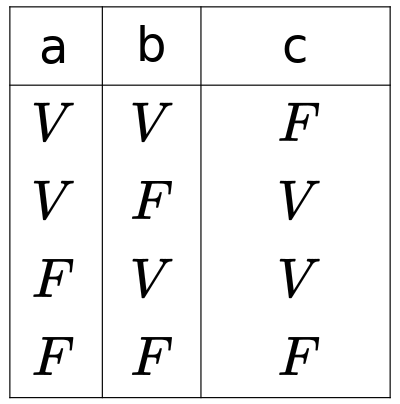
# Conjunción opuesta (NAND)
Esta puerta lógica tiene dos entradas y básicamente activa la salida cuando alguna de las entradas están desactivas, es decir es el operador opuesto al AND. En escritura lo representaremos con la palabra NAND (contracción de "not and" en inglés).
Simbólicamente lo representaremos con el siguiente pictograma:
Eléctricamente es equivalente a:
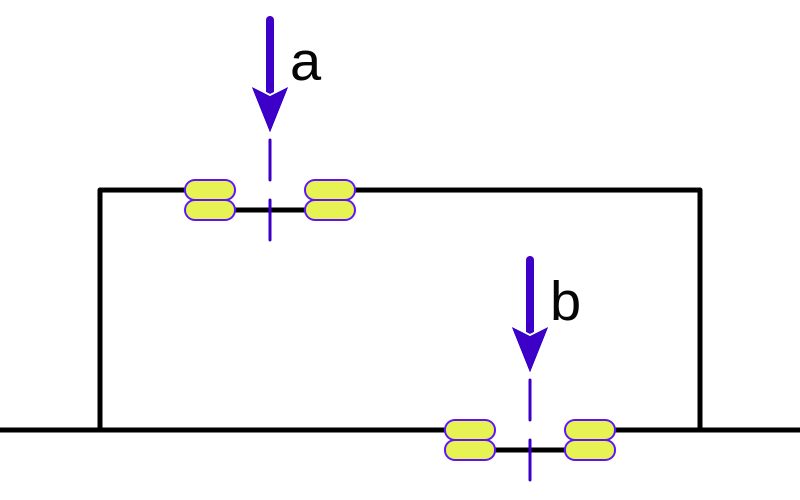
Como vemos se corresponde con dos interruptores en paralelo que se abren al ser activados. Por tanto el circuito se abrirá sólo cando actuemos sobre los dos a la vez.
Su tabla de verdad es:
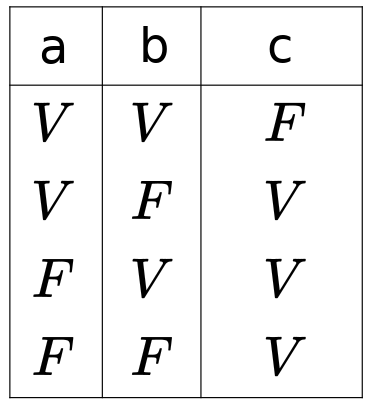
# Disyunción opuesta (NOR)
Esta puerta lógica tiene dos entradas y básicamente activa la salida sólo cuando las dos entradas están desactivas, es decir es el operador opuesto al OR. En escritura lo representaremos con la palabra NOR (contracción de "not or" en inglés).
Simbólicamente lo representaremos con el siguiente pictograma:
Eléctricamente es equivalente a:
Como vemos se corresponde con dos interruptores en serie que se abren al ser activados. Por tanto el circuito se abrirá sólo cando no actuemos sobre ninguno de los interruptores.
Su tabla de verdad es:
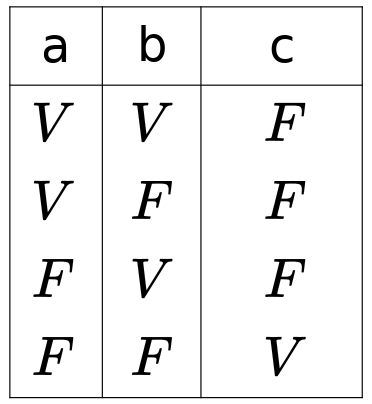
# Puertas lógicas universales
De la enumeración de puertas lógicas anterior, tal vez haya resultado curiosa la presencia en la lista de las NAND y NOR. Al fin y al cabo las otras (NOT, AND y OR) implementan operaciones lógicas "razonables" mientras que estas NAND y NOR pueden verse como extravagantes e innecesarias. Resulta que las dos últimas pertenecen al grupo de las puertas lógicas universales, que son las que permiten implementar todas las demás con combinaciones de ellas. Vamos a ver un par de ejemplos.
# Puerta NOT construida con NOR
Si cortocircuitamos las dos entradas de una puerta NOR de manera que lo convertimos en una única entrada, obtenemos una puerta NOT.
Vamos a demostrarlo viendo cómo queda la tabla de verdad de NOR cuando juntamos las entradas a y b:
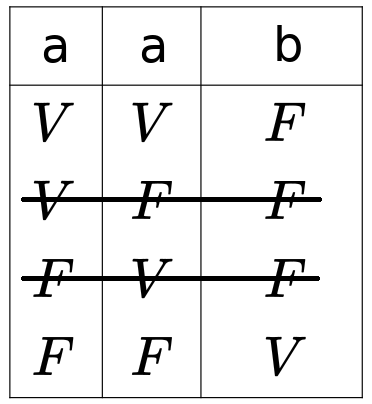
Hemos tachado las combinaciones centrales porque no son posibles en este caso. Como vemos la tabla resultante es completamente equivalente a la de la puerta NOT.
# Puerta OR construida con NOR
La puerta OR, dado que es la contraria a la NOR la podemos construir poniendo una NOT a la salida de una NOR. Pero como acabamos de ver la NOT se puede construir con una NOR cortocircuitando las entradas. Así pues podemos hacer una OR con dos NOR dispuestas de la siguiente forma:
De nuevo vamos a demostrarlo viendo la tabla de verdad:
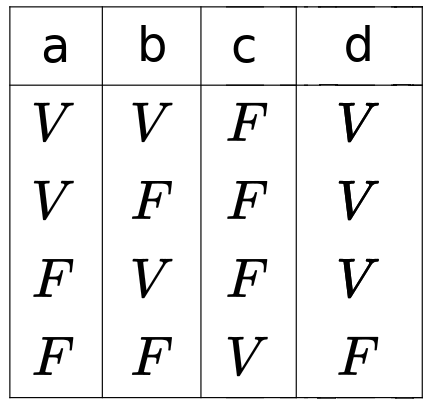
Como vemos, si sólo tenemos en cuenta las entradas a y b y la salida resultante d, obtenemos una tabla equivalente a la de OR.
# Resto de puertas
Aquí tenemos un esquema en el que se muestra cómo se construyen todas las puertas básicas a partir de una NOR:
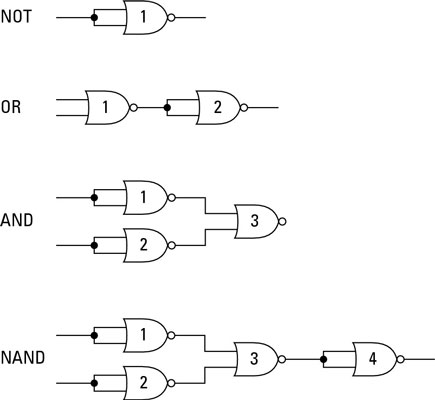
# Conclusiones
Todavía existen más puertas lógicas pero vamos a quedarnos con éstas por ser las más habituales.
Puede que tras haber visto su descripción y comportamiento, se vean sólo como unas aburridas tablas de comportamiento y que todavía no se vea la importancia de estos componentes. La clave está en lo último que hemos visto, es decir que con algunas de ellas se pueden construir todas las demás y en que combinando un número mayor o menor de ellas se puede implementar cualquier algoritmo.
Insistir en que estos operadores están, en forma microscópica, en la base de todos los sistemas digitales, lo que hoy en día es prácticamente como decir en todas partes, ya que la electrónica analógica ha sido casi completamente sustituida por la digital.
