Sistema binario
# Introducción
La mayoría de las veces las personas utilizamos el sistema decimal o en base 10 para representar los números enteros (números sin decimales). Este sistema se basa en combinar 10 dígitos que en la escritura occidental son los símbolos del 0 al 9. La representación de todos los números enteros (como por ejemplo 426, 16, 9963, etc.) se produce con combinaciones de estos 10 dígitos. Esto es así fundamentalmente porque tenemos 10 dedos en manos y pies, pero es una elección arbitraria que seguramente hubiera sido diferente de haber tenido un número de dedos diferente o haber elegido otro elemento de nuestra fisionomía o del exterior para codificar los números.
Otro buen candidato a haber sido elegido como base para los números es el 12. De hecho tenemos una palabra para él (docena) y está presente en gran cantidad de sistemas humanos (las horas del reloj por ejemplo). El origen de la importancia del número 12 seguramente se basa en el hecho de que tenemos 12 falanjes en los dedos más largos que podemos señalar fácilmente con el pulgar. Así resultó sencillo contar hasta 12 con una sola mano.
Pero pueden elaborarse sistemas de numeración basados en cualquier número de elementos. El más básico de todos utiliza tan sólo dos dígitos o cifras y es el más conveniente para los sistemas de computación, ya que éstos no tienen preferencia por ningún sistema en concreto y facilita mucho las cosas para su implementación física.
# Definición
El sistema binario o sistema en base 2, es un sistema de numeración en el que los números se representan utilizando sólo dos cifras. En occidente utilizamos los dos primeros dígitos de los caracteres numéricos, 0 y 1.
Es el sistema de numeración utilizado casi exclusivamente en el mundo de la electrónica y la informática, ya que es la forma más sencilla de trabajar con señales eléctricas (2 niveles: hay o no hay tensión, hay o no hay corriente, conduce o no conduce, pulsado o sin pulsar, etc.).
# Números binarios
Los números que se utilizarán en el sistema binario estarán pues siempre formados con las cifras 0 y 1. A cada dígito o cifra en este sistema se le suele llamar bit (por la contracción en inglés de binary digit). En la película Tron en que el protagonista se introduce en un ordenador y se convierte en un programa informático, se representa un bit en la siguiente escena:
Tras ver la escena, ¿se te ocurre qué falla en esta representación de lo que es un bit, teniendo en cuenta que sólo puede tener dos estados, 0 ó 1?
Si nos fijamos en el sistema decimal, cuando empezamos a contar cosas de menos a más, empezamos por el 0, luego pasamos al 1, al 2 y así sucesivamente hasta llegar al 9. Cuando queremos pasar al siguiente número nos damos cuenta de que se nos han terminado las cifras, así que lo que hacemos es volver a empezar por el 0 e incrementar en 1 la cifra que hay a la izquierda. Delante del 9 no hay ninguna cifra, pero eso es equivalente a que haya un 0 (¿os suena la expresión "vale menos que un cero a la izquierda"?). Es decir 9 es lo mismo que 09 y que 0009. Por tanto la siguiente cifra a 09 es 10. Con los números en binario hacemos lo mismo. La diferencia es que en binario se usan tan pocos dígitos que se nos terminan cada sólo 2 incrementos, por lo que la incorporación de nuevos números (1) por la izquierda es muy frecuente.
La secuencia de conteo con números binarios sería la siguiente. Vamos a poner desde un principio 3 cifras aunque al igual que con los números en base diez, los ceros a la izquierda se podrían retirar:
000: Empezamos a contar en 0.001: Para el siguiente número pasamos a utilizar la siguiente cifra (1).010: Para el siguiente, como se nos han terminado las cifras hacemos como cuando en base diez pasamos del 9 al 10, es decir ponemos en la primera posición otra vez la primera cifra (0) y pasamos a incrementar la segunda posición. Como en esa segunda posición había un 0, podemos incrementarla sin problemas a 1.011: Para el siguiente, al tener 0 en la primera cifra podemos incrementar sin problemas.100: Para el siguiente, intentamos incrementar la primera cifra => no podemos, así que volvemos a 0 y tratamos de incrementar la segunda cifra => no podemos, así que volvemos a 0 y tratamos de incrementar la tercera cifra, cosa que sí podemos hacer esta vez.101110111
Así pues con 3 bits hemos podido contar 8 números distintos. Si necesitáramos continuar nos haría falta un cuarto bit que nos permitiría continuar la cuenta hasta los 16 números distintos. En general con un número N de bits podremos contar 2ⁿ números distintos. Éste es el origen de una serie de números muy populares en informática:
- 2⁰: 1 = 1 en binario
- 2¹: 2 = 10 en binario
- 2²: 4 = 100 en binario
- 2³: 8 = 1000 en binario
- 2⁴: 16 = 10000 en binario
- 2⁵: 32 = 100000 en binario
- 2⁶: 64 = 1000000 en binario
- 2⁷: 128 = 10000000 en binario
- 2⁸: 256 = 100000000 en binario
- 2⁹: 512 = 1000000000 en binario
- 2¹⁰: 1024 = 10000000000 en binario
- 2¹¹: 2048 = 100000000000 en binario
- 2¹²: 4096 = 1000000000000 en binario
- 2¹³: 8192 = 10000000000000 en binario
- 2¹⁴: 16384 = 100000000000000 en binario
- 2¹⁵: 32768 = 1000000000000000 en binario
- 2¹⁶: 65536 = 10000000000000000 en binario
# Conversión decimal a binario
Si queremos convertir un número decimal cualquiera al sistema de numeración binario un método consiste en ir dividiendo el número entre dos e ir anotando los restos hasta que el resultado de la división sea 1. Al terminar cogeremos ese último resultado (tal y como lo hemos definido siempre será 1) y los restos de las divisiones de debajo hacia arriba.
Por ejemplo si queremos convertir el número 28 a binario haríamos lo siguiente:
El número resultante es 11100.
# Conversión binario a decimal
El procedimiento inverso es más sencillo. Así como en el anterior la operación clave era la división, aquí será la multiplicación. El procedimiento es el siguiente:
- Numeramos la posición de los bits del número binario de derecha a izquierda (ojo) y empezando a contar en 0 en lugar de en 1.
- Cada número binario se multiplica por 2 (la base de los números binarios) elevado a la posición del bit obtenida en el paso anterior.
- Sumamos todos los resultados anteriores.
Vamos a aplicar este método por ejemplo al número binario de 6 bit 101101:
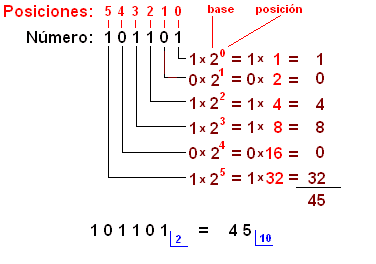
Como vemos el número en base 10 o decimal es el 45.
Ahora que ya sabes contar en binario podrás entender la siguiente camiseta.

